![]() (1)
(1)
Представленный параграф о защите информации основан на книгах [31] - [33], хотя следует отметить, что [34] базируется на замечательном результате Юрия Ивановича Манина (см. [35]), где он дал изящное элементарное доказательство теоремы Г.Хассе о числе решений сравнения (1) (из [34]). Более того, мне думается, что используя результаты [36], можно разработать достаточно большое количество различных новых методик защиты информации, которые будут отличаться одна от другой различной трудоемкостью преодоления их стойкости. И если вести речь о методах защиты, базирующейся на различных соотношениях из теории чисел, то следует учитывать, что оценки такой трудоемкости всегда основываются на последних достижениях по сложностным оценкам.
Последние результаты, в которых показано, что классы задач P и NP совпадают (см. [ПП]), изменили положение в теории сложности. Теперь, с учетом последних результатов, можно сказать, что методики, как разработанные, так и потенциально возможные, основанные на соотношениях из теории чисел, имеют одинаковую сложностную величину, определяемую временем решения задачи ВЫП. Что касается решения задачи ВЫП, то об этом сказано в п. 5 а), даны соответствующие пояснения и проиллюстрированы примером, прилагаемым к этому разделу.
К сказанному можно добавить следующее. Методы, описанные в п. 4 из [31] и в [34] имеют примерно одинаковый сложностной порядок, который диктуется сложностью задачи ВЫП, и вот почему.
Всякий метод, базирующийся на труднорешаемой задаче из теории чисел, как правило, представляет из себя некоторое равенство между алгебраическими выражениями, содержащими переменные и параметры. В таком случае конспективная схема подхода такова. Задача из алгебраической должна быть переведена в логическую, логическая сведена к задаче ВЫП. Сказанное выполняется реализацией следующих пунктов.
1) Переменные и параметры записываются в двоичной системе счисления.
2) Над этими переменными и параметрами выполняются те операции, которые имеются в обоих частях равенства, и, таким образом, наше равенство превращается в равенство, в обоих частях которого имеются записи по степеням двойки.
3) Для того, чтобы можно было приравнять выражения из обеих частей равенства при одинаковых степенях двойки, следует эти записи нормализовать, то есть так их преобразовать, чтобы выражения при степенях двойки равнялись 1 или 0.
4) Нормализованные записи позволяют нам записать систему логических равенств, приравняв выражения из обеих частей равенства при одинаковых степенях двойки.
5) Затем систему логических равенств следует свести к задаче ВЫП, над которой разумно выполнить суперприведение.
Проиллюстрируем эту конспективную схему на задаче факторизации, в которой есть все трудности, требующие преодоления и проще для восприятия и понимания главных сущностей.
Как хорошо известно, задача факторизации состоит в разложении заданного нечетного целого числа a на два простых множителя, то есть найти x и y из равенства
![]() (1)
(1)
С самого начала заметим, что требование, чтобы x и y были простыми нет никакой надобности: достаточно попробовать, чтобы каждый из множителей x и y был больше 1, что равносильно, чтобы каждый из них был меньше a. Тогда, если
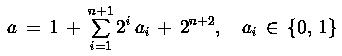 (2)
(2)
то
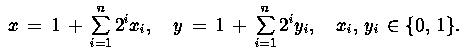 (3)
(3)
Над левыми и правыми частями выражений (3) выполняется умножение и получаем:
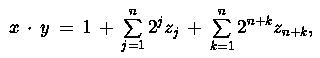 (4)
(4)
где для j = 1, 2, ... , n имеем
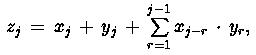 (5)
(5)
и для k = 1, 2, ... , n имеем
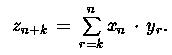 (6)
(6)
Теперь, чтобы выполнить основной пункт 3), следует применить
теорию ![]() -операторов
из [ПП], позволяющую выполнить нормализацию. Чтобы понять, как ее
можно выполнить, ниже приводим без всяких изменений из [ПП] полностью
подраздел
-операторов
из [ПП], позволяющую выполнить нормализацию. Чтобы понять, как ее
можно выполнить, ниже приводим без всяких изменений из [ПП] полностью
подраздел
1.6.1 ![]() -операторы,
где следует иметь ввиду, что для двоичных нуля и единицы
принято обозначение
-операторы,
где следует иметь ввиду, что для двоичных нуля и единицы
принято обозначение ![]() и
и ![]() соответственно.
соответственно.
![]()
![]() -оператором
k-го
класса:
-оператором
k-го
класса:
![]() (7)
(7)
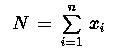 (8)
(8)
совпадает с одним из чисел множества:
![]() (9)
(9)
где ![]()
Отметим, что в соответствии с данным определением ![]() -операторы
- это бесконечные векторы, первые 2k координаты
которых суть
-операторы
- это бесконечные векторы, первые 2k координаты
которых суть ![]() ,
а следующие 2k координаты равны
,
а следующие 2k координаты равны ![]() и далее все периодически повторяется:
и далее все периодически повторяется:
Одно из замечательных свойств ![]() -оператора
(7)
заключается в том, что для него верна следующая очевидная
-оператора
(7)
заключается в том, что для него верна следующая очевидная
Теорема 8. Если число N, определенное в (8), записать в двоичном представлении так:
![]() (10)
(10)
то
![]() (11)
(11)
В том, что это действительно так, легко убедиться, взглянув на таблицу истинности, которую пишем, когда таблично определяем функцию алгебры логики, перечисляя все возможные наборы для аргументов функций.
Разумеется, что вместо бесконечных ![]() -
операторов можно рассматривать конечные
-
операторов можно рассматривать конечные ![]() -операторы
порядка r (предполагая r > k):
-операторы
порядка r (предполагая r > k): ![]() - это операторы, первые 2r координаты которых
совпадают с координатами бесконечного оператора
- это операторы, первые 2r координаты которых
совпадают с координатами бесконечного оператора ![]() k
(обращаем внимание, что в
k
(обращаем внимание, что в ![]() - операторе счет координат начинается с нуля).
- операторе счет координат начинается с нуля).
Замечание 11. Теорема 8 остается верной и для конечных ![]() - операторов (где k = 0, 1 , 2, ... j - 1), если
- операторов (где k = 0, 1 , 2, ... j - 1), если
![]() (12)
(12)
(здесь квадратные скобки указывают на то, что мы берем целую часть действительного
числа ![]() ).
Это значит, что теорема 8 в этом случае слегка изменит свою
форму, точнее, верна
).
Это значит, что теорема 8 в этом случае слегка изменит свою
форму, точнее, верна
Теорема 9. Если число N, определенное в (8), запишется в двоичном представлении так:
![]() (13)
(13)
то
![]() (14)
(14)
Определение (12) показывает, как следует вводить порядок, чтобы
от бесконечных![]() - операторов переходить к конечным. А это значит, что свойства операторов
можно формулировать, учитывая лишь класс оператора и не обращая внимания
на их порядок. С учетом сказанного обратим внимание на то, что верны следующие
теоремы.
- операторов переходить к конечным. А это значит, что свойства операторов
можно формулировать, учитывая лишь класс оператора и не обращая внимания
на их порядок. С учетом сказанного обратим внимание на то, что верны следующие
теоремы.
Теорема 10. Если
![]() (15)
(15)
то
![]() (16)
(16)
Верно и обратное, то есть из справедливости (16) следует справедливость (15).
Теорема 11. Пусть
![]() (17)
(17)
Тогда
![]() (18)
(18)
Верно, что из справедливости (18) следует справедливость равенства (17).
Теорема 12. Если
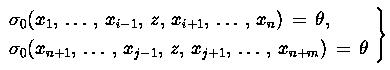 (19)
(19)
то переменная z, входящая в каждое из уравнений системы (19), может быть исключена, то есть
![]() (20)
(20)
Соотношение (20) верно и в том случае, если вместо z иметь z1 , z2 , ... , zs в каждое из уравнений системы (19).
Теоремы 10 - 12 достаточно просты и не могут вызывать
никаких затруднений, поэтому их обоснование опущено. Разумеется, что здесь
не ставилась цель установить все свойства ![]() -операторов, неоднократный возврат к которым предполагается в последующих
главах.
-операторов, неоднократный возврат к которым предполагается в последующих
главах.
А так как над конечными ![]() -операторами
предполагается выполнять логические операции, то ниже рассмотрим
способ их записи, который удобен, поскольку в нем хорошо выражен позиционный
принцип.
-операторами
предполагается выполнять логические операции, то ниже рассмотрим
способ их записи, который удобен, поскольку в нем хорошо выражен позиционный
принцип.
Используя изложенную в 1.6.1 теорию, можно запрограммировать
процесс нормализаций с применением ![]() -операторов.
Далее следует от
-операторов.
Далее следует от ![]() -нотации
перейти к FS-операторам, что позволит получить задачу ВЫП.
Здесь уместно обратить внимание, что приравнивая в (2) и (4)
нормализованные выражения при одинаковых степенях двойки, имеем
уже до процесса нормализации
-нотации
перейти к FS-операторам, что позволит получить задачу ВЫП.
Здесь уместно обратить внимание, что приравнивая в (2) и (4)
нормализованные выражения при одинаковых степенях двойки, имеем
уже до процесса нормализации
zn + k = 0 для всех k > 2.
Последнее заключение, примененное к (6), показывает, что в задаче ВЫП имеется большое количество (больше половины) FS-операторов ранга 2. Отсюда вывод: получается задача ВЫП не самой большой сложности, а мы свои заключения в п. 5 а) всегда ориентируем на задачи максимальной сложности.